We visualize the neutrino oscillation phenomena, observed in solar neutrinos and atmospheric neutrinos, using motions of coupled pendulums. Different kinds of neutrinos obey the same equation of motion as that of coupled pendulums. Taking advantage of this fact, we reproduce and visualize the neutrino oscillation in vacuum and the neutrino oscillation in the Sun (MSW mechanism), respectively, using pendulum experiments (Video show). Furthermore, we present theory backgrounds of these motions.
"Neutrinos" belong to the family of elementary particles, such
as electron and quarks. Presently it is known that there are three different
species of neutrinos: electron-neutrino (![]() ), muon-neutrino (
), muon-neutrino (![]() ), and tau-neutrino (
), and tau-neutrino (![]() ).
).
A neutrino changes into a different species while it proceeds through vacuum. For example, suppose an electron-neutrino propagates in the vacuum; it changes into a muon-neutrino while propagating; it turns back again to an electron-neutrino after some time; and this cycle repeats.
This phenomenon is called oscillation between electron-neutrino and muon-neutrino (neutrino oscillation between different species).
The equation of motion followed by neutrinos propagating in vacuum takes the same form as that of coupled pendulums. (Detailed form will be described below.) We may take advantage of this fact and visualize the neutrino oscillation in vacuum by the motion of pendulums. Because neutrinos are difficult to detect, we cannot see the neutrino oscillation phenomenon directly. Here we may gain image of the neutrino oscillation phenomenon from the pendulum experiment.
|
The video begins from the scene where only the left-hand-side pendulum is oscillating. This state represents that only electron-neutrino exists. Due to resonance effect, the right-hand-side pendulum starts oscillating gradually ( ref 1 ). In terms of neutrino oscillation, this represents that part of the electron-neutrino changed into muon-neutrino. When the amplitude of the right-hand-side pendulum becomes maximum, the left-hand-side pendulum (almost) stops motion. This shows that electron-neutrino turned completely to muon-neutrino. As time goes, the left-hand-side pendulum starts oscillating again; its amplitude increases; soon the amplitude becomes maximum, when the right-hand-side pendulum stops. This shows reappearance of electron-neutrino's component and that after some time the system returns to the initial state (only electron neutrino exists). This oscillation pattern repeats itself further on.
Next we describe neutrino oscillation in the Sun (MSW mechanism).
Electron-neutrinos are copiously being produced close to the center of the Sun through nuclear fusion processes. These electron-neutrinos proceed towards the surface of the Sun, and in the meantime electron-neutrinos turn to muon-neutrinos. This oscillation process in the Sun has an important difference from the neutrino oscillation in the vacuum. As well-known, neutrinos have very high penetrating power and rarely collide with ordinary matters. There exist, however, so dense and large number of electrons/positrons at the center of the Sun, that even electron-neutrinos cannot penetrate freely but collide many times with surrounding electrons and positrons. As a result, electron-neutrinos behave as if they become heavier. (In technical term, we say "electron-neutrinos gain effective mass.") As electron-neutrinos fly away from the center of the Sun, their effective mass reduces because the density of surrounding electrons/positrons decreases accordingly. On the other hand, even if there are muon-neutrinos in the Sun, they do not collide with electrons or positrons, so their mass are unchanged ( ref 2 ).
The equation of motion followed by electron-neutrinos and muon-neutrinos in the Sun takes the same form as that of a special type of coupled pendulums. View the video below:
The right-hand-side pendulum represents the electron-neutrino component, while the left-hand-side pendulum represents the muon-neutrino component. We increase the length of the right-hand-side pendulum gradually while it oscillates; this corresponds to the fact that effective mass of electron-neutrinos reduces gradually as they proceed away from the center of the Sun. We see no resonance effect when the two pendulums have very different lengths. As their lengths become close to each other, the left-hand-side pendulum starts to oscillate by resonance effect. After some time, when the right-hand-side pendulum becomes sufficiently long, ideally the right-hand-side pendulum stops and only the left-hand-side pendulum oscillates. (In the video, the right-hand-side pendulum is still moving slightly, though.) Namely, originally there were only electron-neutrinos at the center of the Sun, but by the time they reach the surface, all of them turned to the muon-neutrinos. The largest difference from the neutrino oscillation in the vacuum is that after electron-neutrinos changed to muon-neutrinos, they do not oscillate back to electron-neutrinos. Maybe one can regard this feature to be plausible after looking at the pendulum experiment.
We explain the equation of motion and the behaviors of their solutions further down in this page.
Appendix
We also performed a similar pendulum experiment, which does not correspond to the neutrino oscillation phenomenon in the Sun:
In the beginning only the left-hand-side pendulum is oscillating. Then we increase the length of the right-hand-side pendulum gradually. In this case, the oscillation of the left-hand-side pendulum almost completely transfers to the right-hand-side pendulum. At the end, the left-hand-side pendulum almost ceases oscillation.
Below we supplement the above description by theoretical explanation that
may be appropriate for graduate course students.
Neutrino Oscillation in Vacuum
Two species of neutrinos propagating in the vacuum obey the equation of motion:
 |
(1) |
If we regard ![]() and
and ![]() , respectively, as the angles of two pendulums, this equation is essentially
equivalent to the equation of motion of coupled pendulums.
, respectively, as the angles of two pendulums, this equation is essentially
equivalent to the equation of motion of coupled pendulums.
For example, the solution to the above equation under the initial condition
![]() at
at ![]() is given by
is given by
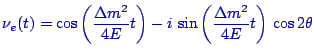 |
(2) | ||
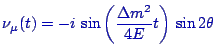 |
(3) |
In this case, the time dependences of the squared-amplitudes of the oscillations are given as follows:
![\includegraphics[width=7cm]{vac-osc.eps}](img10.png)
In terms of motions of the coupled pendulums: At ![]() , the pendulum
, the pendulum ![]() has the maximal amplitude, while the pendulum
has the maximal amplitude, while the pendulum ![]() is at rest. On the other hand, at
is at rest. On the other hand, at 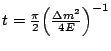 , the pendulum
, the pendulum ![]() is oscillating with the maximal amplitude, while the pendulum
is oscillating with the maximal amplitude, while the pendulum ![]() is at rest. (See the experiment.)
is at rest. (See the experiment.)
In terms of neutrino oscillation, it shows that the initial electron-neutrino
![]() completely turned to the muon-neutrino
completely turned to the muon-neutrino ![]() at
at 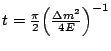 . As time goes further, the electron-neutrino component reappears.
. As time goes further, the electron-neutrino component reappears.
Neutrino Oscillation in the Sun (MSW Mechanism)
The equation of motion followed by the neutrinos in the Sun may be written in the form:
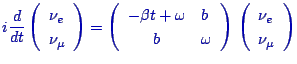 |
(4) |
where,
![]() ,
,
![]() ,
,
![]() .
.
The initial condition is given by ![]() at
at ![]() .
.
The above equation can also be regarded as that of coupled pendulums; since
the frequency of the pendulum ![]() decreases with time, it corresponds to coupled pendulums where the length
of the pendulum
decreases with time, it corresponds to coupled pendulums where the length
of the pendulum ![]() increases with time.
increases with time.
The solution to the above equation is given by
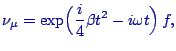 |
(5) | ||
![$\displaystyle \color{blue}
\nu_e = \frac{i}{b} \, \exp (-i\omega t) \, \frac{d}{dt} \biggl[
\exp\Bigl( \frac{i}{4}\beta t^2 \Bigr) \, f \biggr] ,$](img20.png) |
(6) | ||
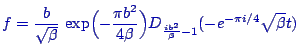 |
(7) |
In this case, the time dependences of the squared-amplitudes of the oscillations
are shown below:
![\includegraphics[width=7cm]{MSW-osc.eps}](img23.png)
(Written by Y. Sumino)